knuth-morris-pratt is smart
this algorithm confused me for a long time and i dont even know why it took so long for me to understand it. so i’m just dumping my understanding of it here, lest i forget it in the (likely) near feature. don’t know if i’ll ever need it though.
when to use? what is this problem?
there might be other applications, but as far as i know, this is a good optimization for pattern matching, or when you want to find a pattern within a big string with a lot of repeated sequences (i.e. DNA sequences). so for this post, assume that we have a big string and we want to find a pattern within it.
the example i’m using is string = "bacbababaabcbab" and pattern = "ababaca".
the partial match table
this is the main part that I was confused about. I thought this was the solution but it’s just a tool to help us find the solution quicker. this is a preprocessing step that goes through the pattern and helps us find shortcuts (later on) by finding the length of the longest proper prefix in the (sub)pattern that matches the proper suffix in the same (sub)pattern.
Take ‘cat’ for example. the proper prefixes is ‘c’, ‘ca’, and the proper suffixes are ‘t’, ‘at’. (in this case, none match).
Each index of the table will look at the substring up to that index (so index 0 looks at ‘a’, index 1 looks at ‘ab’, index 2 looks at ‘aba’, etc.).
Picture above: how i formed the partial match table for ‘ababaca’. the leftmost column is the index, then in red is the actual value (length of the longest prefix that matches the suffix). the orange box boxes the substring that we’re looking at, all text to the left are the prefixes, and to the right are the suffixes. also highlighted in blue the matching prefixes/suffixes.
ok so now what?
here’s the KEY thing: you see, normally, if you’re looking for ‘ababaca’ in ‘bacbababaabcbab’, when you look for matches, you might get pretty far before starting over again with the index right after the start of your current matching window. now, you can use the partial match table to see if you can skip any work! (for example, in a pattern with a lot of repeated characters like catcat and you were looking in a string like catcatcat, after you found the first catcat, instead of starting over with the substring atcatcat, you automatically jump to index 3 and continue with the substring catcat. so much faster!)
every time you get a partial match of length len, and your table[len] > 1, you skip ahead len - table[len-1] steps! here’s another scrappy visual:
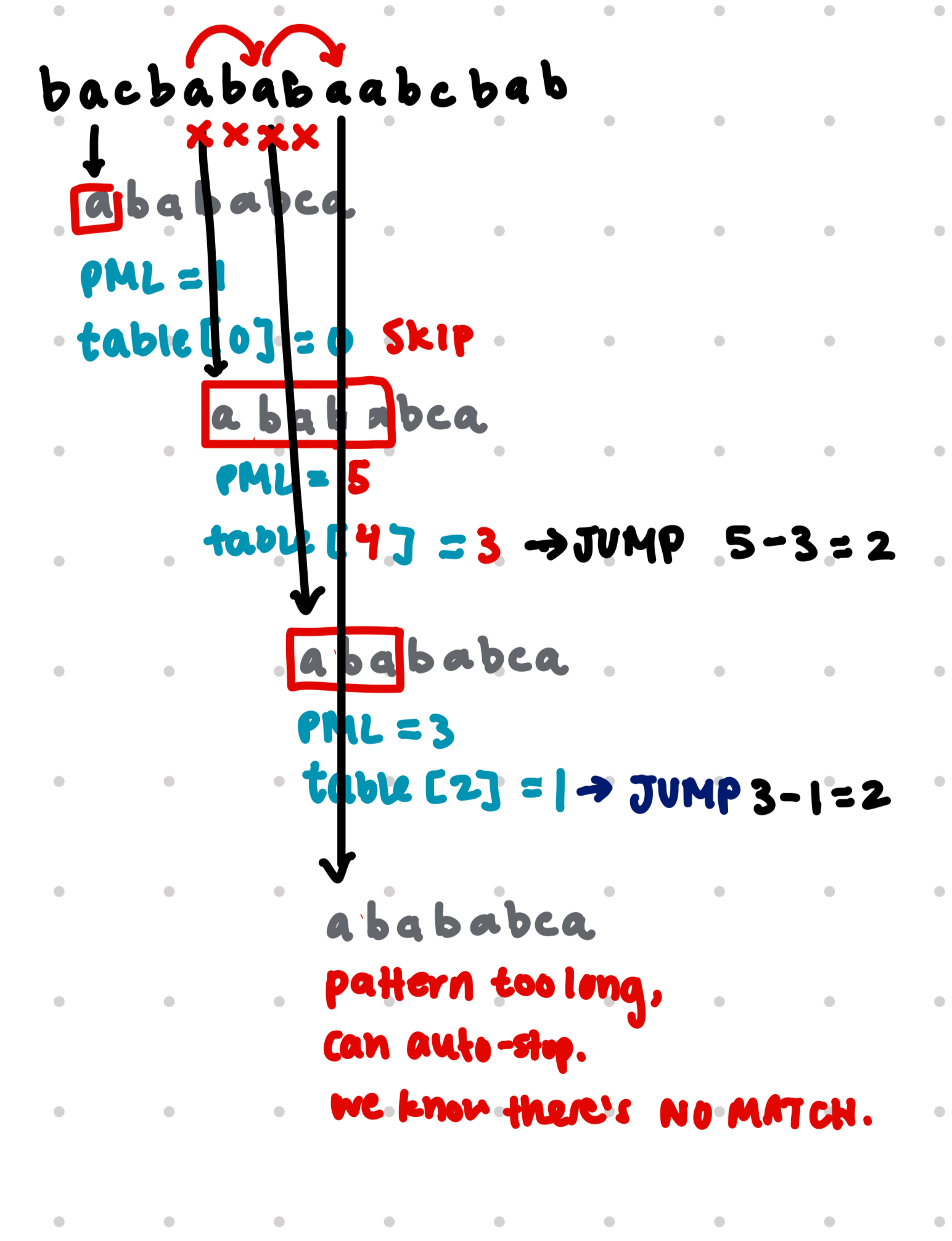
here’s the x’s are the jumps you can make. you can see that for example, when ababa got partially matched to the substring ababaabcbab, instead of starting over with searching the substring babaabcbab, the algorithm directly jumped ahead to abaabcbab (skipped 3 steps), because the ab part of the pattern is repeated (and so the pattern matching algorithm already did that work before). don’t have to do it again!
the runtime is then reduced from O(n*m) to O(n+m), where n is the length of the string and m is the length of the pattern. wowowow!
OR
instead of moving your pointer traversing through the string, you can directly move your pointer (patternPointer) to table[patternPointer-1] and keep your place in the big string the same.
leetcode 28’s a good example: https://leetcode.com/problems/find-the-index-of-the-first-occurrence-in-a-string/
in conclusion, lazy = smart
as my piano teacher once said, the lazy people are the smartest, because they find ways to avoid doing things the hard way. this algorithm is a good example of that – it takes shortcuts so it can avoid redoing work that it’s already done! i suppose that’s the case with a lot of algorithms these days though.
also, the more i write, the more i’m confusing myself so i’m gonna stop here. bye!